


The model presented here was ready, in its fundamental form, in 1992. In the following years, many discussions on the rec.music.early newsgroup, in particular with Margo Schulter regarding Pythagorean tuning and Pierre Funk regarding comma adjustment, allowed me to refine and explain it better. But I would never have dared publish what follows without the providential meeting with Yves Ouvrard and Jean-Pierre Vidal in the summer of 1998. They enthusiastically worked to develop the software tool of my dreams, one I would never have been able to create alone. May they find here the expression of my gratitude.
In the second part of his Istitutioni Harmoniche 1, Gioseffo Zarlino provided what constitutes one of the first precise descriptions of a musical temperament 2. At the end of this analysis, he devoted a chapter to vocal intonation, declaring in a manner which could not be more clear, that a cappella singers tend not to use a particular temperament but rather intervals in their "true form" 3. This assertion made him the prophet 4 of what later theoreticians have called "just intonation" 5. Rather than a proof, which he hardly had the means to demonstrate, it is a credo which he espouses. He posits an ideal 6, not necessarily achieved, but nevertheless highly desirable. Careful to refer to his elders for support, he identified the system he promoted with one of those proposed by Ptolemy in the second century. The name of this theoretician of antiquity was chosen to balance that of Pythagoras, traditionally associated with the only accepted tuning system of medieval theory.
If one is interested in instrumental intonation, one can find invaluable instruction as well as technical treatises on the instruments themselves, or representative tables 7. However, Zarlino's profession of faith is, along with the controversy it provoked (notably between Zarlino and his former student Vincenzo Galilei 8), the only starting point available to us for approaching the intonation of 16th century singers.
Some have always considered just intonation to be a total fantasy. They see in it, perhaps with reason, a mathematician's whimsy lacking real musical content. Nevertheless this "illusion" has been the object of a quest for a long time, a quest which Haynes readily compares to that for the Grail 9. If there were a point in space-time where this quest had a chance to bear fruit, it would have been in one of the high-level cappelle or camerate which flourished in 16th century Italy, the microcosm which saw "all the practitioners, transformed by Zarlino's authority" 10 diligently in search of the best possible intonation. It was at this time more than at any other that just intonation could have been the object of a more or less conscious and reasoned practice.
Moreover, such an assertion would gather strength if just intonation were other than a vague idea. Putting it into practice implies, in effect, choices which could lead to very different outcomes. One can search in vain in early or modern writings for procedures enabling its application to concrete musical examples. What we are attempting to describe here is certainly not a set of rigid instructions, but above all a reference framework which we wish, although it is not absolutely essential, could be of practical use today. If Renaissance singers employed a form of just intonation, what would have been their implicit or explicit strategies, whether conscious or unconscious, for coming close to such an ideal? This then is the fundamental question which we are asking ourselves. We will thus be led to ask ourselves another, more burning question, especially in a time when numerous vocal ensembles have dedicated themselves to Renaissance polyphony: In what way should today's singers who want to adopt Zarlino's ideal proceed to attain it? We suggest that the two questions have the same answer, in that the answer to the second is unnecessary if profound thought has already gone into answering the first.
After having been rather forgotten, just intonation came back into fashion with the naturalism of the Romantic era, in particular through the work of the great physicist Helmholtz, who used a "just harmonium" for his experiments in tuning. While promoting universal application of his "natural scale" by singers and violinists of his time, he considered it particularly appropriate for Renaissance music:
The characteristics of the natural scale are most evident in the early Italian music of Palestrina, Vittoria, Gabrieli, and their contemporaries. These works require very accurate consonance because they produce their delicate harmonic effects only through chord inversions, the alternation of major and minor chords, and the small number of dissonances caused by suspensions. When performed in a tempered scale, they lose all meaning and expression. However, when played on the harmonium using the natural scale, they can produce a pleasing effect. 11
He also recognised that the singers he heard were, for the most part, incapable of singing "in a way that gives the listener this total well-being which comes from perfect harmony." This incapacity he attributed to the harmful influence of the pianos with tempered tuning with which they practised. Things were quite different in the past:
Until the seventeenth century, singers were taught by means of a monochord, for which Zarlino, in the middle of the sixteenth century, had rediscovered the true natural scale. 12
But what then is this "True Natural Scale" for which Zarlino really should, his own views notwithstanding, assume the responsibility? Without entering into the detail of Helmholtz's discussion, which is based on a very idiosyncratic modal nomenclature, we can recognise what he called the "Major Scale." This he describes by the following frequency ratios 13 :
ut1 - re - mi - fa - sol - la - si - ut2
1 - 9:8 - 5:4 - 4:3 - 3:2 - 5:3 - 15:8 - 2This scale, included ad infinitum in dozens of more or less recent theoretical works, under various names such as Zarlino's Scale, the natural scale or the physicists' scale, has supported numerous definitive judgements, from those on just intonation to those on Zarlino himself. What are we to think of it? Above all, that we are involved here with a major anachronism. No matter what one might think after superficial examination of a figure (Figure 1.1) appearing in his treatise, Zarlino could in no way have "rediscovered the natural scale," for the simple reason that the concept of scale and its corollary, of key or tonality, did not exist at the time of the Renaissance. However, that must not prevent us from pursuing the examination of what we will call from now on Helmholtz's scale, in order to review some basic ideas on the calculation of musical intervals.
All the degrees of this scale form simple frequency ratios with its tonic ut, corresponding to what are called "pure" intervals 14: ut1-ut2 forms an octave with a ratio of 2; ut1-sol a fifth with a ratio 3:2; ut1-fa a fourth with a ratio 4:3; ut1-mi a major third with a ratio 5:4; ut1-re a tone with a ratio 9:8; la-ut2 a minor third with a ratio 6:5; si-ut2 a semitone (diatonic) with a ratio 16:15.
Difficulties appear as soon as we calculate the intervals which appear between the intermediate degrees, and in particular the seconds, the fifths and the thirds. First of all, the seconds re-mi and sol-la have a ratio 10:9, leading to the definition of a minor tone. This requires us to rename the traditional or Pythagorean tone of 9:8 to major tone. Such a distinction between a minor tone and a major tone is missing from the principal systems of intonation prevalent historically in music for keyboards (Pythagorean tuning, meantone, and equal temperament). Moreover, the rules of counterpoint and later, of harmony, never took it into account. Furthermore, with the fifth re-la we find the ratio of 40:27, an interval which if played would offend even the least delicate of ears. In comparison with the fifth of 3:2, it is too small by a micro-interval, which comes to 81:80, and which we call a syntonic comma (hereafter just a comma, for short). Lastly, the minor third re-fa has a ratio of 32:27, which is in fact a Pythagorean minor third. It will be noted that it is also the comma which makes the difference between a major tone and a minor tone, as well as between a Pythagorean third and a pure third.
In order to mitigate the effect of these irregular intervals, due to the intrusion of an unavoidable "grain of sand" called a comma, Helmholtz introduced a second re in his scale, a comma lower than the first 15. This made it possible to restore to their "natural" ratios the fifth re-la and the minor third re-fa, and with this duplicated note, it became possible to create perfect chords within Helmholtz's scale. This cleared the way for tonality. But it is then reasonable to wonder whether a scale which offers an optional degree is still a scale, and moreover how will it be able to function as a diatonic framework if one of its degrees is indeterminate? Which alternative re does one choose when ascending from ut to mi? One also wonders how to leave this narrow domain of absolute "tonal purity," because the least modulation would introduce other Helmholtz scales, each one as indeterminate as the next. How would a singer be able to find pitch? And, even admitting that he has succeeded, how does one imagine that, on the basis of such an anachronistic premise, he could get even slightly close to the frame of mind which prevailed in the Renaissance? It is with this impasse that we will abandon the search for the "natural scale."
The Pythagorean diatonic system, as described by Boethius and medieval theory, is already a form of just intonation. It is built up solely on simple proportions, utilising factors of 2 and 3. All the intervals which make it up are "untempered" and can be reduced to combinations of octaves (ratio of 2:1) and fifths (ratio of 3:2). Adopted by those who tuned keyboard instruments, it was arbitrarily limited to a cycle of twelve fifths, the last of which, the famous wolf, too small by a Pythagorean comma, reflected the mathematical impossibility of finding an integral power of two equal to an integral power of three. This is equivalent to the impossibility of making a given number of fifths coincide with a given number of octaves. In reality, if we reject arithmetical compromises, and also leave the octaves out of consideration, a series of pure fifths will appear not as a circle but as a spiral extending indefinitely in both directions. It is this spiral which constitutes the kernel of any system of just intonation. Unrolled, it takes the following form 16 :
...Ebb-Bbb-Fb-Cb-Gb-Db-Ab-Eb-Bb-F-C-G-D-A-E-B-F#-C#-G#-D#-A#-E#-B#-F##-C##-G##-D##-A##...
The principal limitation of this system is that it does not make it possible to generate pure major thirds (5:4) or minor thirds (6:5), but only the Pythagorean thirds of 81:64 and 32:27. We recall that the major Pythagorean third is a comma (a syntonic comma) greater than the pure major third; the minor Pythagorean third is a comma smaller than its pure counterpart. The ingenious step, shown in particular by Barbour 17, is taken by adding, parallel to this primary series of pure fifths, a second series "-1" shifted a comma lower. This makes it possible to generate pure major thirds starting from each note of the first series. For example, on a short length:
series "-1" : ... D-1 A-1 E-1 B-1 F#-1 C#-1 G#-1 D#-1 ...
/ \
primary series: ... Bb --- F --- C --- G --- D --- A --- E --- B --- F# ... Starting from any note in the primary series (for example C) and moving diagonally up to the right, we obtain the pure major third (E-1 is a comma below the E of the primary series). Going down again diagonally towards the right, we arrive at G, a fifth from the starting note C. This completes the major triad. More generally, having added a series "-1" of fifths, one can find, from each note of the primary series, the major third by going higher into the series "-1" and the minor third by going lower. (G to B-1, major third; G to E-1, minor third).
But all of our problems are not yet solved. In order to be able to generate, for each note of the primary series, major thirds by going lower and minor thirds by going higher, it is now necessary to add a series of fifths "+1" to the system, shifted a comma higher:
series "-1": ... D-1 A-1 E-1 B-1 F#-1 C#-1 G#-1 D#-1 ...
/ \
primary series: ... Bb --- F --- C --- G --- D --- A --- E --- B --- F# ...
\ /
series "+1": ... Db+1 Ab+1 Eb+1 Bb+1 F+1 C+1 G+1 D+1 ... By going down diagonally towards the right, and returning similarly, it is now possible to obtain any minor triad. The combination of these three series of fifths thus makes it possible to generate, from each note of the primary series, a major triad and a minor triad. This may seem satisfactory, but what occurs if, starting from a note of one of the added series, one wishes to generate a new pure third? One must then have recourse to an additional series of fifths, shifted by a further comma compared to the preceding one. This implies the possibility of an infinite set of series, both upwards and downwards:
...
series "-3": ... A#-3 E#-3 B#-3 F##-3 C##-3 G##-3 ...
series "-2": ... F#-2 C#-2 G#-2 D#-2 A#-2 E#-2 B#-2 ...
series "-1": ... D-1 A-1 E-1 B-1 F#-1 C#-1 G#-1 D#-1 ...
/ \
primary series: ... Bb --- F --- C --- G --- D --- A --- E --- B --- F# ...
\ /
series "+1": ... Db+1 Ab+1 Eb+1 Bb+1 F+1 C+1 G+1 D+1 ...
series "+2": ... Fb+2 Cb+2 Gb+2 Db+2 Ab+2 Eb+2 Bb+2 ...
series "+3": ... Abb+3 Ebb+3 Bbb+3 Fb+3 Cb+3 Gb+3 ...
... This then is finally a "complete system for the generation of pure chords," to adopt the phrase of Asselin 18. This network represents all the frequencies it is possible to reach while moving by combinations of pure fifths and thirds, starting from a fixed point (for example A at 440 Hz). It is impressive because it extends indefinitely in four directions. Each series of fifths can extend to the left and the right indefinitely, while it is also possible to add further series of fifths both above and below the primary series (series -1; +1; etc.). If we also remember that we left the octaves out of consideration in the first stage, we can now reintroduce them. Imagine that the whole complex two-dimensional diagram above is transposed by an octave. This new diagram can be placed on a new sheet of paper (or a new screen) parallel to and above the existing surface. This process can then be repeated indefinitely, both upwards and downwards in pitch, so as to give access to all the frequencies attainable by combinations of pure octaves, fifths, and thirds - in theory. (Theory is not limited by considerations of human hearing or vocal range!) We can appreciate that such a structure was able to induce a feeling of vertigo in some authors, such as D. Devie, who nevertheless provided a very colourful description:
One can imagine an immense labyrinth formed by a building of many storeys. At each level a corridor in the form of a spiral unwinds to infinity in concentric circles towards the periphery. Every five metres we find a stairway leading up to the next storey above, or down to the next storey below. These represent the pure thirds. Consider that we represent the most trivial perfect interval within this labyrinth, and we gain some idea of the absurd character of the system in question. 19
This sense of vertigo comes primarily from the incredible richness of different frequencies derivable from such a labyrinth, and the impossibility of conceiving a keyboard capable of providing them. Attempts in this direction have led to many curiosities of instrument manufacture, which have never gone beyond the prototype stage 20.
Vertigo of a different kind attacks the singer who tries to enter the labyrinth of Barbour. The voice, being extremely flexible, is not subject to the main weakness of keyboard instruments - a limited number of keys in each octave. If nevertheless a singer loses his way, it is primarily because he does not know how to move from one note to the next. In other words the labyrinth of Barbour only allows movement by thirds, fifths and octaves and is totally deficient as a diatonic framework. There is no way it can indicate how to move by degrees. The interval of a second, elementary link in all melodies, never appears directly.
Lacking a better solution, Barbour 21,
well aware of the weaknesses of the Helmholtz scale and its inherent
unsuitability as a diatonic framework, relied upon what we might call
the principle of the common note. He suggested that, where a
note is common to two consecutive chords, the pitch of that note must
not change. The result is that certain sequences of chords
introduce a pitch instability 22
which, should the phenomenon repeat itself, can become a real drift.
He took the following example: 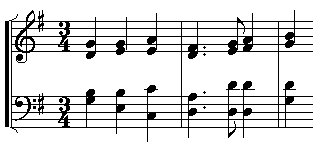
Figure 1.2 : The opening of God save the King.
If we accept that the pitch of the A of the fourth chord must
be the same as that of the third, then the G major chord which ends
this extract becomes a comma flatter than the opening chord. If we
repeat these first two bars of the famous anthem in a loop, we get a
curious descent to the nether regions (Example
1.1) 23.
It is enough, it seems to us, to hear this just once in order to
accept it as unsatisfactory. No vocal group, whether modest or
excellent, would wish to reproduce such a "submersion," and
even less to use it as a model.
Systematically applied, the principle of the common note, or any other analogous principle, will produce drifting of pitch in many pieces, in exactly the same way as in God save the King. Barbour used this observation to construct a fundamental refutation of just intonation. In strict logic, it is only the principle of the common note which this observation could have nullified. Strangely, that has not been the case. The same principle has been revived since, in a more general form, and precisely by those in favour of just intonation. Amongst the specialised interpreters of vocal polyphony, it is not unusual to hear the opinion (in our view far-fetched) expressed that if one sings "truly" just, then the pitch "must" fluctuate. Such an opinion on this point is sufficiently accepted that one finds it taken up again in recent theoretical papers 24. If we suggest, a trifle ironically, that it is certainly more gratifying for a group of singers to tell themselves that they sound out of tune because they sing "too" justly than to admit that they sing badly or "not quite" justly, then we can better begin to understand the growth of such a myth.
But what we are missing here, nevertheless, is that the principle of the common note, and consequently the drift of pitch, are by no means unavoidable. There is no reason why the tenor singing God save the King must inevitably take over his A of the fourth chord from the A sung by the soprano in the third chord, thus forcing the other voices to follow him in dropping pitch. Why can we not expect the alto and the bass to move to the D already present in the initial chord (in tonal terms, the dominant) while the soprano joins them by singing a descending pure third, A-F (the solution of the common note would require her to sing a Pythagorean third here)? In this case, the three voices would drive the tenor to tune his A a comma upwards from the one he anticipated. Is this second solution, on paper, harder to believe than the first? It has the advantage of maintaining the pitch level as well as the vertical purity, and even if repeated in a loop, is not distressing to the ear (Example 1.2) . How can it be justified that the first solution, which "sounds false," is taken as representative of just intonation, while the second, which "sounds true," is excluded from this definition?
How are we to advance in the face of all these questions? We need to examine Zarlino and the theories of the sixteenth century.
| Summary | Introduction | Chap. 1 | Chap. 2 | Chap. 3 | Chap. 4 | Conclusion | Bibliography |